日々のあれこれとか、同人とか、プログラミングとか、3DCGとか。不定期に書きつづってます。
[1]
[2]
完全な事後報告なことこの上ない感じ。
実は、先週のコミックマーケット82にて、制作中のゲームの体験版を配布していました。
サークル参加した「Tri-Niv」のスペースでやっていました。
当日はタブレットでプレイ動画を再生していましたが、足を止めてくれた方、体験版を
持って行ってくれた方、ありがとうございました。
あ、Tri-Nivスペースで配布してましたが、制作は自分の個人サークルの「七月の三日月」って
ことにしています。分かりにくいことこの上ないですが……
制作には、年明けからいじっていたUnityを使っています。
なので、プログラミングらしいプログラミングは実はやっていなかったり。
しかしまあ、作っているのは決してUnityらしいゲームではないので、ちょっと無理して
実装してある部分もありますが……
以下、ちょっとばかり紹介。
ユーザーの操作はうどんげをジャンプさせる1操作のみ、ワンボタンで遊べる簡単な
アクションゲームです。
うどんげが月を目指してどんどん昇っていくゲームとなっています。
体験版では、タイトル画面とキャラ選択画面とゲーム部分しか無いですが、完成版では
もっとゲームらしく肉付けする予定。
タイトル画面。

ゲーム画面1。
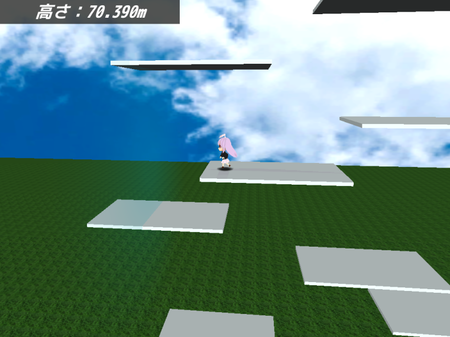
ゲーム画面2。
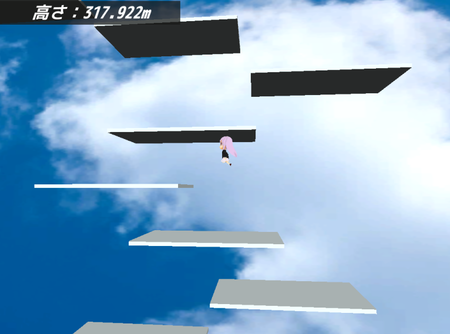
イラストはサークルTri-Nivで一緒に活動している猫犬ユッキー氏(Pixiv)に描いてもらいました。
冬コミには完成できるよう頑張っておりますので、生暖かく見守っていただければと思います。
実は、先週のコミックマーケット82にて、制作中のゲームの体験版を配布していました。
サークル参加した「Tri-Niv」のスペースでやっていました。
当日はタブレットでプレイ動画を再生していましたが、足を止めてくれた方、体験版を
持って行ってくれた方、ありがとうございました。
あ、Tri-Nivスペースで配布してましたが、制作は自分の個人サークルの「七月の三日月」って
ことにしています。分かりにくいことこの上ないですが……
制作には、年明けからいじっていたUnityを使っています。
なので、プログラミングらしいプログラミングは実はやっていなかったり。
しかしまあ、作っているのは決してUnityらしいゲームではないので、ちょっと無理して
実装してある部分もありますが……
以下、ちょっとばかり紹介。
ユーザーの操作はうどんげをジャンプさせる1操作のみ、ワンボタンで遊べる簡単な
アクションゲームです。
うどんげが月を目指してどんどん昇っていくゲームとなっています。
体験版では、タイトル画面とキャラ選択画面とゲーム部分しか無いですが、完成版では
もっとゲームらしく肉付けする予定。
タイトル画面。
ゲーム画面1。
ゲーム画面2。
イラストはサークルTri-Nivで一緒に活動している猫犬ユッキー氏(Pixiv)に描いてもらいました。
冬コミには完成できるよう頑張っておりますので、生暖かく見守っていただければと思います。
PR
ちょっと違う気がするけどUnity関連はプログラミングカテゴリで。
そしてプログラミングカテゴリはいろいろ放り出したまま途中のものもありますが、
Unityに関しては放り出さないよう頑張ります。
この本を買ってちょっとずついじっていますが、本当に簡単にはじめられるのでびっくり。
3Dのキャラを操作してカメラで追っかけるくらい、すぐ作れちゃうのねー。
というわけで、Unityで何か作れるように、勉強進めていこうと思います。
そしてプログラミングカテゴリはいろいろ放り出したまま途中のものもありますが、
Unityに関しては放り出さないよう頑張ります。
この本を買ってちょっとずついじっていますが、本当に簡単にはじめられるのでびっくり。
3Dのキャラを操作してカメラで追っかけるくらい、すぐ作れちゃうのねー。
というわけで、Unityで何か作れるように、勉強進めていこうと思います。
今日はタイトルの通り、「変換行列からオイラー角を求める方法」でハマってしまい、
えらい時間が掛かったので、自分メモのつもりで投稿。
変換行列からオイラー角による回転を計算する場合、回転順序によって6種類の
計算方法があります。
(ちなみに、回転順序はXYZ、XZY、YXZ、YZX、ZXY、ZYXの6種類です。)
ちなみに、ベースとなる情報元は以下のwiki。
http://www7.atwiki.jp/lucifer/pages/13.html
ここの解説の仕方をベースに、誤っていると思われる部分を修正した表にしておきます。
まず、変換行列は以下の形になっているという前提。
最初の回転軸をα、2番目の軸をβ、3番目の軸をγとすると、各回転順序での計算方法は
以下のようになります。
ただし、cos(β)がゼロになる場合は、α=0、β=90又は-90としてγを計算しなおします。
上の表の計算方法を使えば、各回転順序でオイラー角を取得出来るハズ。
ただ、浮動小数で計算していると、三角関数や除算なんかで不正値がでたり
するのでそっちも注意が必要。
例えば、if (cos(β)==0) みたいなコードにしちゃうと、cos(β)の結果が非常に小さい
値だけどゼロで無い時に、cos(β)での除算結果が不正値になったり。
ふう。自分メモ終了。
自分以外にも誰かの役に立ったりしたら幸いです。
えらい時間が掛かったので、自分メモのつもりで投稿。
変換行列からオイラー角による回転を計算する場合、回転順序によって6種類の
計算方法があります。
(ちなみに、回転順序はXYZ、XZY、YXZ、YZX、ZXY、ZYXの6種類です。)
ちなみに、ベースとなる情報元は以下のwiki。
http://www7.atwiki.jp/lucifer/pages/13.html
ここの解説の仕方をベースに、誤っていると思われる部分を修正した表にしておきます。
まず、変換行列は以下の形になっているという前提。
| m00 | m01 | m02 | ||
| 行列R | = | m10 | m11 | m12 |
| m20 | m21 | m22 |
最初の回転軸をα、2番目の軸をβ、3番目の軸をγとすると、各回転順序での計算方法は
以下のようになります。
| α | β | γ | γの角度 | βの角度(-90~90) | αの角度 |
| X | Y | Z | atan2(m01,m00) | asin(-m02) | asin(m12/cos(β)) if(m22<0) α=180-α |
| X | Z | Y | atan2(-m02,m00) | asin(m01) | asin(-m21/cos(β)) if(m11<0) α=180-α |
| Y | X | Z | atan2(-m10,m11) | asin(m12) | asin(-m02/cos(β)) if(m22<0) α=180-α |
| Y | Z | X | atan2(m12,m11) | asin(-m10) | asin(m20/cos(β)) if(m00<0) α=180-α |
| Z | X | Y | atan2(m20,m22) | asin(-m21) | asin(m01/cos(β)) if(m11<0) α=180-α |
| Z | Y | X | atan2(-m21,m22) | asin(m20) | asin(-m10/cos(β)) if(m00<0) α=180-α |
ただし、cos(β)がゼロになる場合は、α=0、β=90又は-90としてγを計算しなおします。
| α | β | γ | γの角度 | βの角度(-90又は90) | αの角度 |
| X | Y | Z | atan2(-m10,m11) | asin(-m02) | 0 |
| X | Z | Y | atan2(m20,m22) | asin(m01) | 0 |
| Y | X | Z | atan2(m01,m00) | asin(m12) | 0 |
| Y | Z | X | atan2(-m21,m22) | asin(-m10) | 0 |
| Z | X | Y | atan2(-m02,m00) | asin(-m21) | 0 |
| Z | Y | X | atan2(m12,m11) | asin(m20) | 0 |
上の表の計算方法を使えば、各回転順序でオイラー角を取得出来るハズ。
ただ、浮動小数で計算していると、三角関数や除算なんかで不正値がでたり
するのでそっちも注意が必要。
例えば、if (cos(β)==0) みたいなコードにしちゃうと、cos(β)の結果が非常に小さい
値だけどゼロで無い時に、cos(β)での除算結果が不正値になったり。
ふう。自分メモ終了。
自分以外にも誰かの役に立ったりしたら幸いです。
ここ最近、プログラミング熱が熱くなっています。
モデリングやイラスト描きそっちのけでやっている感じ。
(だって、プログラマなのに、仕事であまりプログラミングできないんだもの。最近。)
プログラミングの内容は、3DCG関連。かなり基礎からおさらいな感じ。
DirectXでXファイルのビューワプログラムなどちまちま作っていました。
上のスクリーンショットのような感じ。
自分で作ったモデルが、自分のプログラムで表示されるのは、なかなか
面白いものですね。
それにしても、DirectXをラップして自分好みの3Dライブラリもどきを作って
満足しないようにしないと。
何かしら、世に出せるミニゲーム的なものでも作りたいですね。
あと、DirectInputをラップして、入力回りは整えてあるので、後はDirectSoundで
音再生回りをモジュール化してしまいたい。
さらに、GWの休み中にはPhysXに手をだしてしまいたい……!
さてどうなるやら。
さっそく少しだけ横道にそれて、COLLADA DOMに同梱のCOLLADAビューワに
ついて少しだけ。
親切な事に、COLLADA DOMにはビルドするだけで使えるCOLLADAビューワが
同梱しています。COLLADAファイルの内容を軽くチェックするのに非常に便利。
■1 ビルド準備
COLLADAビューワのビルドには、NVIDIAのCg Toolkitが必要になります。
下のURLから最新版をダウンロード、インストールしておきましょう。
http://developer.nvidia.com/object/cg_toolkit.html
自分がダウンロードした段階では、Cg Toolkit2.2 (February 2010)が最新版でした。
念のため、動作確認済みのCg Toolkit2.2 (February 2010)は以下のURLから
ダウンロードできます。
Cg Install PackagesのWindowsのところのDownloadから。
http://developer.nvidia.com/object/cg_2_2_feb10.html
■2 ビルド方法
COLLADAビューワの一式は、COLLADA DOMの以下のディレクトリにあります。
(DOM-PATH)\viewer
さらに、以下のディレクトリに各環境のソリューションファイルがあるので、開きます。
自分の環境では、vc9-Winディレクトリのものを使用しました。
(DOM-PATH)\viewer\projects
Cg Toolkitのインストールが済んでいれば特に問題なくビルド成功するハズ。
COLLADA DOM自体のビルドと同様に、C4819の警告が頻発するので、お好みで
無視するよう設定してください。
ビルドが成功すると、以下の実行ファイルが出力されます。
(DOM-PATH)\viewer\bin\viewer-d.exe (デバッグ版)
(DOM-PATH)\viewer\bin\viewer.exe (リリース版)
■3 使用方法
ビューワの実行ファイルに、適当なCOLLADAファイルをドラッグ&ドロップする
ことで、ビューワが起動してCOLLADAファイルの内容が表示されます。
ちなみに以下のzipファイル内にサンプルのCOLLADAファイルがあるので、
解凍して使ってみても良いでしょう。
(DOM-PATH)\viewer\bin\samples.zip
使用方法は、(DOM-PATH)\Readme.txtの230行目辺りから書いてあります。
当然英語なので、よく使うものは以下にメモ。
左ドラッグ オービット(視点の回転)
右ドラッグ トラッキング(視点の平行移動)
ホイール回転 ドリー(視点の前後移動)
Q ワイヤーフレーム表示
P アニメーションの一時停止
さて次回こそは、COLLADA DOMを使ったアプリの作り方で。
カレンダー
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tri-Niv過去作品DL販売
【地霊 DE Collection】
(DLsite.com)
【(株)地霊ででーんでん!-C92-】
(DLsite.com)
【地底 summer vacation 2013】
(DLsite.com)

(DLsite.com)
【(株)地霊ででーんでん!-C92-】

(DLsite.com)
【地底 summer vacation 2013】

(DLsite.com)
プロフィール
HN:
文月大 (ふみづき・だい)
性別:
男性
カテゴリー
最新記事
(2026/01/03)
(2026/01/02)
(2025/12/31)
(2025/12/01)
(2025/11/24)
最新コメント
[2016/09/11 shougo_k2100]
[2015/10/25 cstdlib]
[2014/06/11 shougo_k2100]
[2011/09/10 文月大]
[2011/09/07 リコ]
最新トラックバック
多目的スペース
ブログ内検索
広告

